№
|
Название
|
Вид уравнения
|
Даны
|
1
|
Каноническое
уравнение прямой
|
(x - x0) / a1 = (y - y0) / a2
|
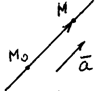
Точка M0(x0,y0) и направляющий
вектор a = {a1 , a2}
|
2
|
Уравнение прямой
проходящей через
две точки
|
(x - x1) / (x2 - x1) =
= (y - y1) / (y2 - y1)
|
Две точки M1(x1,y1) , M2(x2,y2)
|
3
|
Уравнение прямой
В отрезках
|
x / a + y / b = 1
|
Две точки M1(a,0) , M2(0,b)
|
4
|
Общее уравнение
Прямой
|
Ax + By + C = 0
где C = - ( Ax0 + By0)
|
Точка M0(x0,y0) и нормальный
вектор n = {A , B}
|
5
|
Уравнение прямой
с угловым коэффи-
циентом
|
y = k x + b
|
Угол пересечения оси Ох -
Смещение по ординате - b
k = tg = 2 1
|



Примеры решенных задач

Темы, по которым я решаю задачи:
- Линейная и векторная алгебра
- Аналитическая геометрия
- Математический анализ
- Комплексные числа
- Неопределенный и определенный интегралы
- Функции нескольких переменных
- Дифференциальные уравнения
- Двойные, тройные, криволинейные и поверхностные интегралы
- Ряды (числовые, степенные, Фурье), интеграл Фурье
- Теория поля
- Теория функции комплексного переменного
- Операционное исчисление
- Теория вероятностей
- Математическая статистика
- Теория случайных процессов

Уравнение прямой линии
Понятие прямой линии - первичное в геометрии. Свойства прямой определяются аксиомами геометрии. Геометрически построить линию можно разными способами :
Задать две точки на плоскости.
Задать одну точку M0(x0 ,y0 ) и направляющий вектор a
Задать одну точку M0(x0 ,y0 ) и нормальный вектор n
Задать одну точку и угол наклона к оси Ox .
Каждому из этих способов задания прямой линии соответствует своя форма уравнения.
Вывод уравнения прямой линии.
1. Заданы точка M0(x0 ,y0 ) и направляющий вектор a = {a1,a2}.
1) Пусть M(x,y) - произвольная точка прямой.
2) Общее свойство : любой отрезок прямой, в том числе и вектор М0М , коллинеарен вектору a , т.е. М0М=kа
3) Переход к координатной форме этого условия
(x - x0) i + (y - y0) j = (a1 i + a2 j)
Из этих равенств следует каноническое уравнение прямой:
(x - x0 )/a1 = ( y - y0 ) /a2 ( 1 )
2. Заданы две точки M1(x1,y1) и M2(x2,y2) на прямой.
Вектор М1М2 может служить направляющим вектором
М1М2= a = {x2 - x1 , y2- y1}
и тогда каноническое уравнение прямой переходит в уравнение прямой проходящей через две точки
(x - x1) / (x2 - x1) = (y - y1) / (y2 - y1) ( 2 )
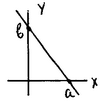
Если заданы точки пересечения прямой с осями координат
М1(a,0) и М2(0,b), то получаем уравнение прямой в отрезках
x/a + y/b = 1 ( 3 )
3. Заданы точка M0(x0 ,y0 ) и нормальный вектор n = {A,B}.
1) Пусть M(x,y) - произвольная точка прямой.
2) Общее свойство : любой отрезок прямой, в том числе и вектор М0М , перпендикулярен вектору n, т.е. nМ0М = 0
3) Переход к координатной форме этого условия
(A i + B j) [(x - x0) i + (y - y0) j ] = 0
дает уравнение прямой проходящей через точку с заданным нормальным вектором
A (x - x0) + B (y - y0) = 0 ( 4 )
а выражение
A x + B y + C = 0 , где C = - (A x0 + B y0) ( 5 )
называется общим уравнением прямой. Имея такое уравнение, можно сразу записать координаты нормального и направляющего векторов прямой: n ={A,B}, a ={1/A , -1/B}. Последнее равенство
следует из сравнения записи общего и канонического уравнения.
4. Задана точка M0(x0 ,y0 ), а направляющий вектор a ={a1,a2}не определен.
В этом случае каноническое уравнение преобразуется в уравнение пучка прямых, проходящих через заданную точку.
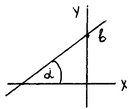
y - y0 = (a2/a1) (x - x0) y - y0 = k (x - x0) ( 6 )
где k = a2/a1 = tg - угловой коэффициент и - угол пересечения прямой с осью Ох. Если для прямой определено k и заданная точка лежит на оси Оу , т.е. M0(x0 ,y0) M0(0,b), то получаем уравнение прямой с угловым коэффициентом.
y = k x + b ( 7 )
Итог: семь форм уравнения прямой линии получены.
При решении задач надо прежде всего определить каким геометрическим способом задана прямая и выбрать для неё соответствующую форму уравнения
В настоящее время я делаю авторские цветы из шелковой ткани. Поэтому, приглашаю на сайт, где вы можете заказать броши на платье, заколки, украшение к свадьбе, вечерние аксессуары.
В другие регионы возможна пересылка цветов по почте.